Monday, June 29, 2020
Coin rotation paradox #3
Saturday, June 27, 2020
Tusi couple
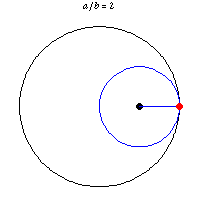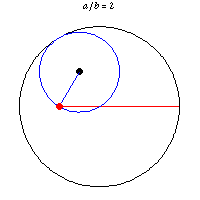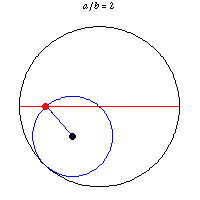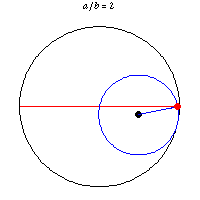
Monday, June 22, 2020
Coin rotation paradox #2
The formula R/r + 1 is correct. However, the reference – author Y. Nishiyami – doesn't give the formula, much less prove it is true for any R and r. Also, Nishiyama says, “Separating revolution from rotation is helpful for understanding, but doing so does not provide a fundamental solution.” This latter part is not true. For a coin with radius r to make one revolution around a stationary coin with radius R, the center of the moving coin travels a circular path with radius R + r. (R + r)/r = R/r + 1. Likewise, the circumference of the path is 2*pi*(R + r)/(2*pi*r) = R/r + 1 times the circumference of the revolving coin. Rotation is irrelevant. [End]
Friday, May 29, 2020
Coin rotation paradox
Analysis and Solution
From start to end the center of the moving coin travels a circular path. The edge of the stationary coin and said path form two concentric circles. The radius of the path is twice either coin's radius. Hence, the circumference of the path is twice either coin's circumference. To go all the way around the stationary coin, the center of the moving coin must travel twice the coin's circumference. How much the moving coin rotates around its own center en route, if any, or in what direction – clockwise, counterclockwise, or some of both – has no effect on the length of the path. That the coin rotates twice as described above and focusing on the edge of the moving coin as it touches the stationary coin are distractions.
At the time of writing this, there is a warning that says the page lacks citations and has unsourced material. Like I said above, I did not find anything to cite or use as a source. I solved it on my own.
Wikipedia can be edited at any time by almost anybody. I hope nobody removes or ruins the above section. Anyway, I hereby document it in my blog, which is far less subject to being altered by others.