Coin rotation paradox #3

I again edited the Wikipedia article about the coin rotation paradox (link) to add two references. One was to the book Mathematical Fallacies and Paradoxes and the other to a YouTube video about when the two circles are different sizes. I also removed the template message about the article lacking sources. 

Tusi couple

Obviously the center of a circle rolling along a straight line travels a straight line. But I had not imagined that a point on the perimeter of a rolling circle could travel a straight line. It can and does if a circle rolls within another circle twice as big. This was noted by a 13th century Persian astronomer and mathematician. Tusi couple.

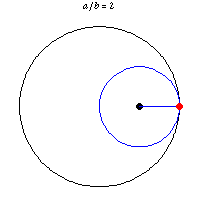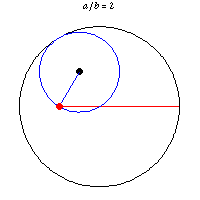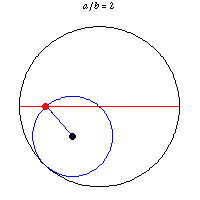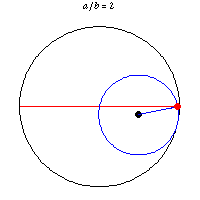
The same attribute with eight points on the perimeter of a rolling circle traveling straight lines is shown here, here (YouTube), and here (YouTube). The last gives some mathematical analysis. Guessing, the "illusion" is that the moving circle is imaginary in the two YouTube videos, since the moving dots are not connected to one another. Part of the first YouTube video shows the dots being added one at a time. The illusion is a rolling square while there are only four dots. 

Meaning of 'Black Lives Matter'

Per Wikipedia "Black Lives Matter (BLM) is an organized movement advocating for non-violent civil disobedience in protest against incidents of police brutality against Afro-American people." 

So a more accurate, more honest, non-racist name would be People Against Police Brutality. I'm for that. If all the phrase BLM meant is that black people also have rights -- to life, liberty, property, the pursuit of happiness, vote, seek political office -- that would be fine with me. I suspect that is the way many people view it and what gives the phrase its broad appeal. However, the organization and movement BLM is far more than that. They are Marxist, racist (anti-white), and pro-violence. Link. Killing people such as David Dorn, destroying property, and looting are neither civil nor non-violent. Two of BLM's founders, Patrisse Cullors and Alicia Garza, are self-admitted Marxists and racists. 

In the USA 93% of Afro-American homicide victims are killed by other Afro-Americans (link). However, I don't see BLM protesters protesting those victims, and I see nothing about it on the BLM website. So apparently their lives mattered little or none.

*****

In The New York Times Michael D. Shear -- who previously worked 18 years for the Washington Compost -- wrote: "In the interview, Mr. Pence called Mr. Floyd’s death “a tragedy,” but his insistence that “all lives matter” is likely to be seen as a provocation by activists and others who say that phrase dilutes the issue and fails to acknowledge the specific threats that African-Americans still face at the hands of police officers in the United States" (link). 

Shear claims that a guy named Taff pressed VP Pence to say "black lives matter" more than once, but Pence would say only "all lives matter." 

Pandering to BLM, both Shear and Taff failed to acknowledge the meaning of "all." "All" includes white, black, Asian, Hispanic, and every other possibility. Shear also ignores (1) the African-American homicide victims killed by other African-Americans, and (2) the specific threats that African-Americans still face at the hands of other African-Americans. When Shear believes it's fair to criticize Pence for what Pence doesn't say, he made it fair to criticize Shear for what he doesn't say.

I did a search for 'what does black lives matter mean?' The following are typical.

This page says, "At its most basic level, it calls for a shift in the statistics that Black people are twice as likely to be killed by a police officer while unarmed, compared to a white individual."

What about "while armed"? What about "killed by another Black person"? Dead silence.

This page says, "So, if you’re unsure about what ‘Black Lives Matter’ means, how to respond to someone when they say ‘All Lives Matter’ or just curious to know why saying ALM doesn’t benefit anyone, let us explain.  ...  The statement is not political or controversial. It’s an expression that calls out for justice, respect and empathy for every life that has been affected by discrimination, prejudice and misrepresentation for centuries. Point blank: It’s raising awareness for basic human rights."

Okay, but "every life" and "basic human rights" aren't limited to black lives; it includes whites, Asian, Hispanics and all other possibilities. 

The same page also shows a picture of woman with an ALM poster, on which "All" doesn't mean "all." Apparently, like Shear and Taff, she doesn't know the meaning of "all," which means each and every one.

The term Word Nazi come to mind. By that I mean somebody who is fond of declaring what another person means when said person uses a particular word or term, regardless of what that person actually means.

Coin rotation paradox #2

Four months ago I edited the Wikipedia article about the coin rotation paradox (link), adding the new section Analysis and Solution. I explained why the moving coin does what it does. I wrote about it on this blog here May 29.

More recently somebody else (user name Cmglee) added another section about one coin revolving around another, but the two coins having unequal radii. While the person gives the correct formula, why it is correct is not explained. The person also gave a reference, but the reference neither gives the formula nor explains why it is true for any two radii. Therefore, I added a new section to the Wikipedia Talk page as follows.

The formula R/r + 1 is correct. However, the reference – author Y. Nishiyami – doesn't give the formula, much less prove it is true for any R and r. Also, Nishiyama says, “Separating revolution from rotation is helpful for understanding, but doing so does not provide a fundamental solution.” This latter part is not true. For a coin with radius r to make one revolution around a stationary coin with radius R, the center of the moving coin travels a circular path with radius R + r. (R + r)/r = R/r + 1. Likewise, the circumference of the path is 2*pi*(R + r)/(2*pi*r) = R/r + 1 times the circumference of the revolving coin. Rotation is irrelevant. [End]

The key to this solution is to focus on the center of the moving coin. The center travels a circular path with radius R + r and hence circumference 2*pi*(R+r) in order to make one full revolution around the stationary coin. How many rotations it makes, even zero, while doing so is irrelevant. (Rotation versus revolution.) If it "rolls without slipping or sliding," then the number of rotations will also be R/r + 1. 

True Plight of Black Americans

Walter Williams' article The True Plight of Black Americans is well worth reading.

Democrats are very fond of accusing others of racism. But what have they done when in charge? They have dominated politics in large cities for decades. What is the result? "Democratic-controlled cities have the poorest-quality public education despite their large, and growing, school budgets."

Such cities are also high crime areas. Williams touches on crime and African Americans. There is more. 93% of African American homicide victims are killed by other African Americans. African Americans accounted for 52.5% of all homicide offenders from 1980 to 2008 (link), despite being only about 13% of the USA's population.

Incoherence of COVID rules

The mayor of Orland Park noticed how incoherent the COVID shutdown rules in Illinois were. 

Who is "taking a knee" for David Dorn?

Chicago Tribune columnist John Kass asks, "Will anyone take a knee for retired police Capt. David Dorn? 

"Dorn, 77, was a retired St. Louis police captain. The other night, as violence raged in St. Louis, Dorn was alerted to an alarm at a friend’s pawnshop. He did what law enforcement officers are expected to do. Dorn answered the call. He tried to stop a gang of looters."

Dorn was shot to death, as much or more unjustly than George Floyd. Dorn was African-American. Didn’t his life matter, too? But there aren’t any protests for Dorn, no public kneeling in his memory. 

Leftists take a knee for George Floyd, who had a long criminal record and spent time in jail for armed robbery. But they don't for Dorn, who was not a criminal. Dorn isn't worth mention on the Black Lives Matter website.

Several other people have died as a result of the protests, looting, and violence in memory of Floyd (link). Don't their lives matter?

Merlin Bird ID App

Hey, I made this app to identify birds. Just kidding, TheCornellLab made it. Somebody told me about it since my first name is Merlin.  About merlins.

I downloaded it to my smart phone (cost $0) and tested it. Neat.

Miracle Sudoku

This video shows a guy named Simon Anthony solving a Sudoku puzzle with only two digits given. He and his partner have a very popular YouTube channel called Cracking the Cryptic. Anthony proceeds to solve the puzzle in about 20 minutes. His feat is impressive, especially with the extra rules he was given. In a common Sudoku puzzle, a solution cannot be unique with so few digits given. I have read that at least 17 or 18 digits are needed for that.  

Anthony’s full solution was as follows with the two given numbers in green.

4	8	3	7	2	6	1	5	9
7	2	6	1	5	9	4	8	3
1	5	9	4	8	3	7	2	6
8	3	7	2	6	1	5	9	4
2	6	1	5	9	4	8	3	7
5	9	4	8	3	7	2	6	1
3	7	2	6	1	5	9	4	8
6	1	5	9	4	8	3	7	2
9	4	8	3	7	2	6	1	5

His solution has recurring trios in the rows of every band and columns of every stack. For example, he entered 4 8 3 in rows 1-3 and 6 9 3 in columns 4-6. The order of digits within some trios aren't all the same. For example, there are 1 4 7 and 7 1 4 and 4 7 1.

I believed I might solve it faster using the copy and paste method I described in my May 27 post, with maybe a little tweaking after filling the grid.

The first digits I entered were as follows. I did the trio 2 6 1 first, then 4 8 5 and 7 3 9. 

4	8	5	2	6	1
2	6	1
7	3	9				2	6	1

Then I filled the rest of the grid as follows, which shows many recurring identical trios.

8	5	4	6	1	2	3	9	7
6	1	2	3	9	7	8	5	4
3	9	7	8	5	4	6	1	2
4	8	5	2	6	1	7	3	9
2	6	1	7	3	9	4	8	5
7	3	9	4	8	5	2	6	1
5	4	8	1	2	6	9	7	3
1	2	6	9	7	3	5	4	8
9	7	3	5	4	8	1	2	6

I finished this full grid in only 3 minutes, 36 seconds. It satisfies the king's move and knight's move rules. However, it violates the other extra rule. Pairs of successive digits appear next to one another, e.g. 1 2 and 4 5. I tried tweaking to get rid of them, but gave up after 20 minutes. 

Mr. Anthony's solution might be unique. Swapping rows 1&2 or rows 8&9 violate the knight's move rule. Hats off to him. 

Sudoku Making

I recently wrote three posts about how to start with a blank 9x9 Sudoku grid and completely fill it with numbers and no guesswork. I showed three basic methods. I thought of more since then that I won’t present. 

A Sudoku puzzle may be described as made of three 3x9 "bands" and three 9x3 "stacks," as demarcated by the lines in the grid below. More puzzles can be made from any full 9x9 grid by: 

- swapping two rows in a band
- swapping two columns in a stack

- reordering bands or stacks
- rotating the entire grid 90, 180, or 270 degrees 
- flipping the entire grid top to bottom or right to left
- transposing around the SW-NE diagonal or NW-SE diagonal. 

All of my methods produce a grid with recurring trios. Such recurring trios do not appear in solutions to puzzles I’ve seen made by others. That is, puzzles with blank spaces masking the full solution and available in newspapers or books, on the Internet, etc. Such recurring trios would also seem to make the puzzle easier to solve.

The following is the first puzzle I showed on May 17. There are recurring trios in the rows of every band, e.g. 3 6 9, and columns of every stack, e.g. 2 3 4.

1	4	7	2	5	8	3	6	9
2	5	8	3	6	9	4	7	1
3	6	9	4	7	1	5	8	2
4	7	1	5	8	2	6	9	3
5	8	2	6	9	3	7	1	4
6	9	3	7	1	4	8	2	5
7	1	4	8	2	5	9	3	6
8	2	5	9	3	6	1	4	7
9	3	6	1	4	7	2	5	8

The following is the second puzzle I showed on May 17, the one above after shuffling digits. It appears more random because 1 2 3 has been replaced by 6 4 7, and 3 4 5 by 7 2 8, and so forth. Yet there are still recurring trios in the rows of every band and columns of every stack. The digits are different, but the locations are the same. 

6	2	9	4	8	1	7	3	5
4	8	1	7	3	5	2	9	6
7	3	5	2	9	6	8	1	4
2	9	6	8	1	4	3	5	7
8	1	4	3	5	7	9	6	2
3	5	7	9	6	2	1	4	8
9	6	2	1	4	8	5	7	3
1	4	8	5	7	3	6	2	9
5	7	3	6	2	9	4	8	1

I have since found ways to eliminate the recurring trios by rearranging a few numbers in the grid. The logic for doing so is rather complicated, but not trial & error. After such rearranging, the scrambler I described on May 17, or the transformations described above, could be used with the grid to create more puzzles with no recurring trios.

Part of the logic is shown as follows. Suppose the top band looks like the following. (It is the first stack above transposed.)

1	2	3	4	5	6	7	8	9
4	5	6	7	8	9	1	2	3
7	8	9	1	2	3	4	5	6

Every row in the left box is repeated in the other two. Swap the numbers 3, 6, 9 in rows 1 & 2. The result would be as follows, with the changes made in green. The recurring trios are eliminated without violating any Sudoku rules. 

1	2	6	4	5	9	7	8	3
4	5	3	7	8	6	1	2	9
7	8	9	1	2	3	4	5	6

I suspect professional Sudoku puzzle makers use a different method involving trial & error. Example 1. Example 2. Whatever methods they do use are likely embodied in a computer program that could do all the trial & error very, very quickly. Do such programs screen for repeating trios? I suspect so.

By the way, every Sudoku solution I have ever seen has repeating pairs in 3x3 boxes aligned horizontally ("band") or vertically ("stack"). The following example is from here. 

9	2	8	1	6	7	5	4	3
1	7	5	4	9	3	2	8	6
6	4	3	2	5	8	7	1	9
8	9	6	3	2	5	4	7	1
3	1	4	8	7	9	6	2	5
7	5	2	6	4	1	9	3	8
2	3	9	5	8	4	1	6	7
5	6	1	7	3	2	8	9	4
4	8	7	9	1	6	3	5	2

The pairs 1,7 and 2,8 repeat in rows 1-3; the pairs 1,4 and 8,9 in rows 4-6, the pairs 1,6 and 2,3 in rows 7-9. The pairs 9,1 and 2,4 repeat in columns 1-3; the pairs 5, 9 and 2,4 in columns 4-6, the pairs 1,8 and 2,7 in columns 7-9. Such repeating pairs are impossible to avoid.